One of the most common behaviors of natural systems is critical behavior, which reveals events that follow the power-law rule. Some researchers believe that criticality is a significant clue to recognizing complex systems, a major part of interdisciplinary sciences in the 21st century. It is generally accepted that the brain is the most important complex system in nature and has evolved over millions of years. Neuroscience is one of the fastest growing fields to study this complex organ.

Throughout neuroscience studies, avalanche sizes and their durations have interested scientists. The size and duration of such neuronal avalanches exhibit scale-free (power-law) statistics, which strongly support the “critical brain hypothesis”. In other words, the power-law behavior of the brain provides strong evidence for its critical dynamics, which, in turn, provides a simple explanation for many functional advantages of the brain. These advantages include efficient information storage and transmission, optimal dynamic range, and stability, along with variability.

In this thesis, we attempt to study top-down modeling (dHAN), which can model the brain’s collective features, such as associative thought processes, through its dynamics. The dense homogeneous associative network (dAHN) model of the brain provides a generic model that is independent of individual neuronal dynamics complications and can, therefore, be considered a very general model of the brain with no regard for specifics.

Through statistical analysis and finite-size-scaling methods, we show that a specific balance between inhibitory and excitatory factors is necessary for critical behavior to appear in the systems. Furthermore, our findings demonstrate that if the excitatory strengths decrease enough, the systems shift to sub-critical dynamics with size-independent activity.

Our findings, when compared to experimental data, emphasize the importance of critical behavior in neural networks by a general top-down model, which apparently has no signs of criticality in its dynamics.

Below represents the numerical simulation written in C++ for a network containing 7 neurons.

dHAN Model (Reference Paper)
The dHAN simulation by original paper for 12 nodes. Yellow indicates current active nodes and green represent previous active ones.

dHAN Model (Simulated by C++ coding)
Testing dHAN model for 7 nodes. Nodes 0 and 1 are active at t=0 as initial condition. Yellow indicates current active nodes and green represent previous active ones.

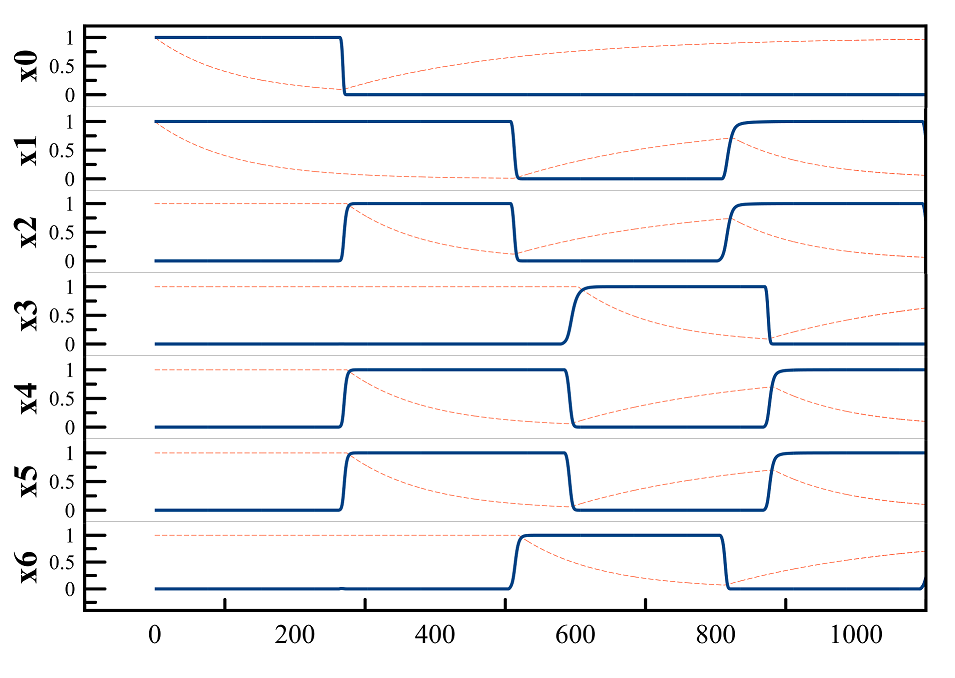
The following figure shows a plot of simulated node activities and their corresponding reservoir functions. The node activities are limited to a range of [0,1] due to the nature of the model. The horizontal axis represents the time step.

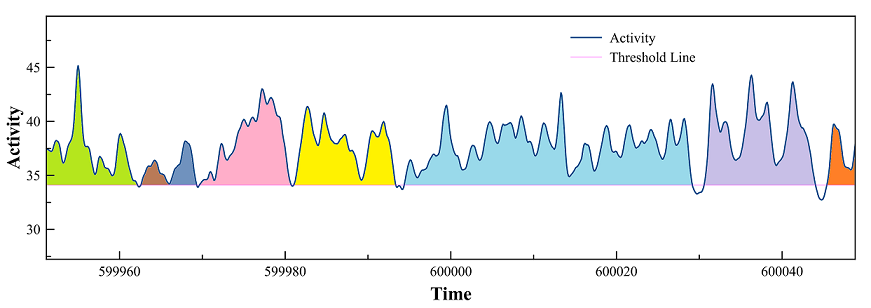
To find criticality in network activities, simulations were repeated for different network sizes, such as 300, 400, and 500 nodes. A threshold line was set for the total network activity to determine avalanche size and lifetime, which were below 95% of the network activity amplitude. The following figure shows how the threshold line was set for this task.
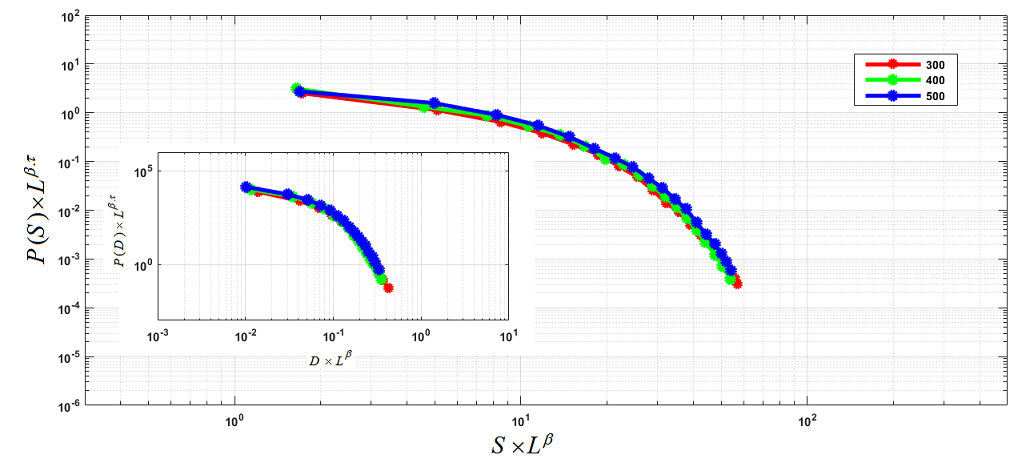
The figure below shows how the avalanche size is distributed in a logarithmic scale for all simulated networks. In this research, we also attempted to tune the connection weight to observe subcriticality and super-criticality.